vol.9 白根 竹人
一般科 准教授
学位 博士(理学)
専門分野 代数幾何学
見えない物を解析する数学
数学の重要性と学ぶ上で大切なこと
数学が重要である一つの理由は「手が届かない物事や目に見えない物事を扱う言語」であるからだと私は考えています。例えば、高専でも習う三角関数は巨大なものの大きさや遠く離れたものの距離を測ることに有効であり、微分積分は物体の軌道や空気の流れの予測に有効であり、天気予報にも用いられています。また、経済においても、様々なデータを数値化することで微分積分などの数学が応用されています。この他にも様々な場面で数学が応用されていますが、数学は観測したデータを用いて現状の解析や未来の予想などを行うための言語となることがその理由の一つだと思います。
数学を学ぶ上で大切なこととして「用語や記号の定義を理解すること」と「2つのものが等しくなる条件を理解すること」の2点があげられます。学校で習う数学は計算を行うだけの学問のように感じる方もいるかもしれませんが、数学は上記のように「言語」とみることができます。数学で扱われる用語や記号の定義を理解することは、英語の単語を覚えることと同様に大切なことです。よくわからない部分も記号の定義を見直すと謎が簡単に解けてしまうなんてこともあります。また、数学における「計算」は「等しくなる条件」を用いて単純な形に変形することなので、その条件を理解していなければなりません。例えば、実数や文字式の計算法則で「交換法則 AB=BA」がありますが、高専でも習う「行列」では交換法則は成り立ちません(一般に、行列 A と B に対して AB≠BA)。つまり、どの体系で考えているかによって「等しくなる条件」が変わるので、正確にその条件を理解する必要があります。その他にも、「2つのものを比較する」ことも数学ではよく行われ、等しくなる条件を理解していなければ比較はできません。

以上では、数学が社会で応用されている理由と数学を学ぶ上で大切なことについて私の考えを述べてきました。さらなる数学の話題として、コンピューターの基礎となる「有限体」の話や摩訶不思議な定理「バナッハ=タルスキの定理」などがあげられますが、以下では、私の研究について大雑把に説明したいと思います。理解が難しい部分もあるかもしれませんが、上記で述べた「見えない物事を扱う言語」と「2つのものを比較すること」が私の研究でも表れていることが伝われば幸いです。
4次元空間について
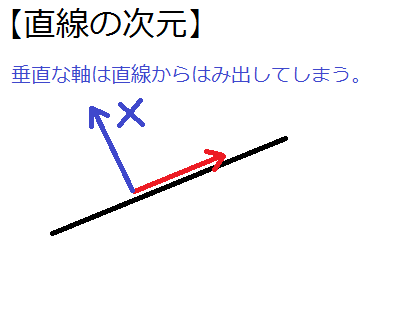
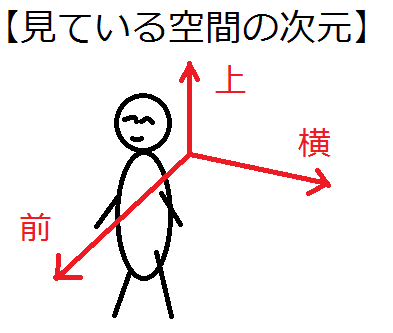
私の研究では4次元空間が現れるので、数学における「次元」について説明します。ある物体や空間のある点での「次元」とは、その点で互いに直角に交わる軸の最大数のことです。例えば、直線上の点では、軸は1つしか取れませんので次元は1、つまり1次元の空間です。我々が見ている空間では、自分を中心に前、横、上と3つの軸がとれ、4つ目の軸を付け足そうとしてもどれか1つの軸とは垂直にならないので、次元は3、つまり3次元空間です。では、4次元空間は存在するのでしょうか?そして、存在していたらどうなっているのでしょうか?
4次元の存在についてですが、数学において、ある物事が「存在する」とは「矛盾なく定義できる」ことを意味します。(例えば、2乗して-1になる数の存在に頭を悩ませた人もいるかもしれませんが、数学では矛盾なくそのような数を定義できるので存在することになります。)4次元の空間の例は次のように定義できます。4つの実数の組(x,y,z,w)を点とする空間にうまく「直角」を定義することにより、x軸、y軸、z軸、w軸の4つの軸を持つ4次元空間ができます。(「直角」についても矛盾なく定義できればよく、高専でも習う「内積」を自然に拡張することで定義できます。)同様に、5次元、6次元とさらに大きな次元の空間を定義することができます(つまり、数学的に存在する)。このように、4次元の空間は数学的に存在しますが「実際には見えない空間」です。
 |
 |
 |
直線上に互いに垂直な軸は一つしか取れないため、直線の次元は1である。 |
前、横、上に3つの軸が取れるが、4つ目の軸を加えると垂直に交わらない軸の組ができてしまうので、見ている空間は3次元である。 |
目では見えないが、数学的には存在する。 |
さて、見えない空間を定義して意味があるのか?と疑問に感じる人もいるかもしれません。しかし、我々が住む空間において、時間を加えて考える、つまり、前(x軸)、横(y軸)、上(z軸)の3つの軸に加えて時間の軸(t軸)を考えた時空は4つの実数の組(x,y,z,t)が点となるので、4次元空間と考えることができます。さらに、その地点の温度、湿度、明るさ等の情報を加えることで、より大きな次元の空間を定めることができます。このように、現実にある情報を並べることで高い次元の空間ができるので、そのような空間を扱う数学には意味があります。そして、このような高い次元の空間を扱うには数学が必要になります。
4次元空間内の2次元物体の絡まり方の違い
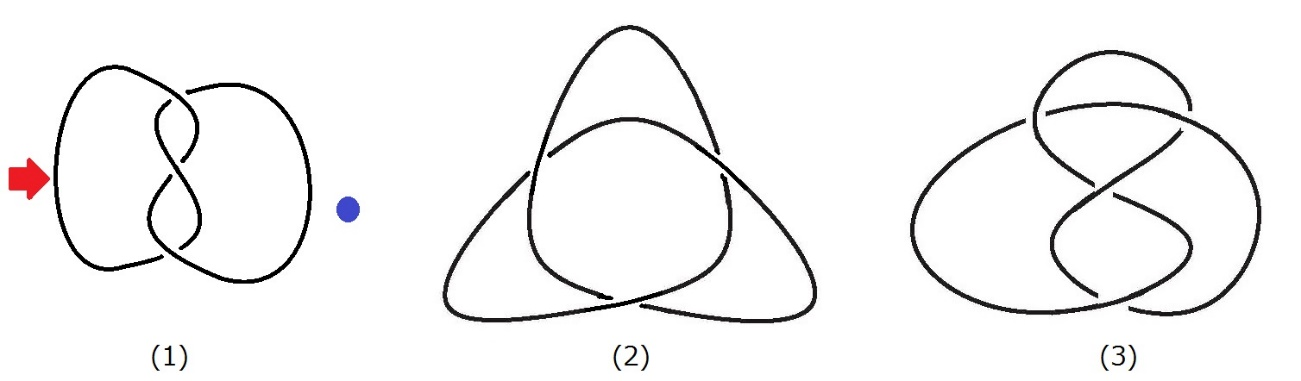
私の研究を大雑把に説明すると「4次元空間内の2次元物体の埋め込まれ方の違いを検出する研究※」です。ここでは、埋め込まれ方と絡まり方は同義であると考えて差し支えありません。ある空間内の物体の埋め込まれ方を説明するために、3次元空間内の輪の埋め込まれ方について説明します。「輪」は紐の両端をテープなどでくっつけたものと考えてください。二つの輪の埋め込まれ方が「同じ」であるとは紐を切らずに一方の輪を他方の輪と同じ形にできることと定義します。紐の両端をくっつけて輪を作るときに、紐の絡まり方によって埋め込まれ方が異なる輪ができます。例えば、下図の(1)の輪は紐を切らずに(2)の輪の形になる(下図(1)の赤い矢印の部分を青い点のところに持っていき、形を調整すると(2)の形になる)ので、(1)と(2)の輪は同じです。一方、下図の(2)と(3)の輪は埋め込まれ方が異なります。
ここで大切なことは、どのように2つの輪の埋め込まれ方が異なることを証明するか?ということです。上図の(2)と(3)の輪については「三彩色数」という不変量を用いることで証明できます。「不変量」とは、それぞれの輪にある量(数)を定め、埋め込まれ方が同じ輪であれば同じ量になるもののことです。「三彩色数」とはある条件に従って輪を三色に塗り分ける場合の数で、上図の例では(2)の三彩色数が9で、(3)の三彩色数が3となります。同じ埋め込まれ方であれば、三彩色数は等しくなるので、上図の(2)と(3)は異なる埋め込まれ方になっていることがわかります。(1)と(2)は同じ埋め込まれ方なので、(1)と(3)も異なる埋め込まれ方になっています。
上記の説明では、3次元空間内の1次元物体である輪の埋め込まれ方について説明しました。私の研究では4次元空間内の2次元物体の埋め込まれ方を扱います。4次元空間は見えないので、上記のように埋め込まれ方の違いを検出する「不変量」によって2次元物体の埋め込まれ方を比較します。
※ 正確には、私の研究で扱う4次元空間は「複素射影平面」で、2次元物体は「(既約とは限らない)複素代数曲線」です。
研究成果 ~ 新しい不変量の定義と応用 ~
埋め込まれ方の差を検出するために不変量を定めることが有効です。しかし、ある不変量が同じでも、埋め込まれ方が異なる場合もあります。私の研究では、新たな不変量を定義し、埋め込まれ方の差を検出する精度を上げることを目的としています。その研究成果としては、「分解数」という新たな不変量を定義し、ある条件の下で分解数を計算する公式を与えたことです。その結果として、これまで用いられてきた不変量で埋め込みの差を検出されていなかった例の差を分解数で検出することに成功しました。つまり、分解数という不変量を加えることにより、埋め込まれ方の差を検出する精度が上がったと言えます。今後の目標は、分解数を改良し、埋め込まれ方の差を検出する精度を上げることです。
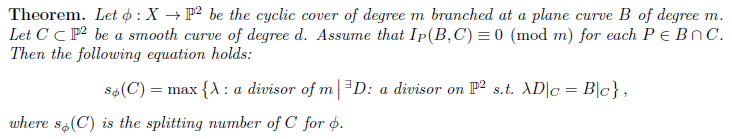
研究成果の公式
最後に ~ 学生へのメッセージ ~

冒頭で述べたように、「見えない物事」を扱うときに数学が有効です。しかし、数学の歴史を考えると、数学の発展の多くは見える世界の法則を定式化することで達成されています。なので、数学を学ぶ上で、身の回りで起きる物事がなぜそのようになるのか考えることがヒントになることもあります。一方、数学では抽象化し、見える世界と離れることで、見える物事からは想像できない現象に出会うことがあり、そんな面も数学の面白いところだと思います。
数学は些細な疑問を放置しておくと、その後の数学が理解できなくなることがある学問です。周りの人が理解しているようでも、疑問感じたことは素直に質問することも大切です。自力で解決できたとしても質問することで、本当に理解できていたか確認ができます。単純なことでも意外と説明が難しいことがよくあります。例えば、(-1)×(-1)=1 を証明するには数の定義を理解しておく必要があり、簡単ではないと思います。宇部高専の数学教員はこのような些細な疑問にも答えることができるので、積極的に質問してください。
現在までの経歴
| 2011年 | 首都大学東京 理工学研究科 博士後期課程 修了 |
|---|---|
| 2011年 | 首都大学東京 理工学研究科 特任研究員 |
| 2013年 | 宇部工業高等専門学校 一般科 講師 |
| 2017年 | 宇部工業高等専門学校 一般科 准教授 |